


Using the Information in this Chapter
Sensitivity Units and Conversions
This chapter contains plots of throughputs and tables of sensitivities and throughputs for each grating mode. Determining Count Rates from Sensitivities explains how to use these sensitivities to calculate expected counts rates from your source.
The first table for each filter provides the following quantities:
Pivot wavelength
|
Source-independent measure of the characteristic wavelength of the bandpass, defined such that it is the same if the input spectrum is in units of f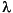 or f or f :
For filters with redleaks, the pivot wavelength and FWHM correspond to the "in-band" region, and do not include the redleak. :
For filters with redleaks, the pivot wavelength and FWHM correspond to the "in-band" region, and do not include the redleak.
|
FWHM
|
Full-width at half-maximum of the throughput T(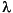 ). ).
|
AB mag zeropoint
|
AB magnitude of a source that produces a flux of one count per second.
|
SPpeak
|
Peak sensitivity (electrons s-1 Å-1 per incident erg cm-2 s-1 Å-1)
|
B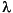
|
Equivalent bandpass of filter, defined such that
 (see Chapter 6).
For filters with redleaks this integration includes only the primary bandpass.
(see Chapter 6).
For filters with redleaks this integration includes only the primary bandpass.
|
Radius for 80% of point source flux
|
Radius in arcseconds of an aperture that encloses 80% of the flux of a point source.
|
% flux in central pixel
|
Percentage of the flux of a point source that falls within the central pixel (this estimate is accurate to about 10%).
|
The first figure for each imaging mode gives the integrated system throughput. This is the combination of the efficiencies of the detector and of the optical elements in the light path.The bottom section of the throughput figures includes wavelengths beyond the nominal passband of that mode, showing any red or blue "leak" on a log scale (dotted sections are manufacturer's lab measurements). The throughput is defined as the number of detected counts per second per cm2 of telescope area relative to the incident flux in photons per cm2 per second. For the CCD "counts" is the number of electrons detected. For the MAMA, "counts" is the number of valid events processed by the detector electronics after passing through the various pulse-shape and anti-coincidence filters. In both cases the detected counts obey Poisson statistics. The throughput includes all obscuration effects in the optical train (e.g., due to the HST secondary and due to the STIS CCD Lyot stops). The "effective area" of the mode can be computed from the throughput by multiplying by the physical area of the HST primary mirror (45238.93416 cm2). This is shown on the ordinate label on the right side of each plot.
The table for each mode gives the throughput and the point-source sensitivity as a function of wavelength. Throughput has the meaning described above. The imaging point-source sensitivity Sp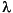 has units of counts sec-1Å-1 per incident erg cm-2 s-1 Å-1 for the MAMAs, and electrons sec-1Å-1 per incident erg cm-2 s-1 Å-1 for the CCDs. Counts and electrons refer to the total counts from the point source integrated over the PSF.
has units of counts sec-1Å-1 per incident erg cm-2 s-1 Å-1 for the MAMAs, and electrons sec-1Å-1 per incident erg cm-2 s-1 Å-1 for the CCDs. Counts and electrons refer to the total counts from the point source integrated over the PSF.
The imaging diffuse source sensitivity, Sd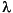 , has the units:
, has the units:
counts sec-1 pix-1 per incident dimensional erg cm-2 sec-1 Å-1 arcsec-2 for the MAMAs and electrons sec-1 pix-1 per incident dimensional erg cm-2 sec-1 Å-1 arcsec-2 for the CCDs.
Thus Sp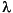 and Sd
and Sd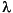 are related through the relation:
are related through the relation:
Where m is the plate-scale in arcsec per pixel. Here, we have assumed that the diffuse source has a uniform brightness over the area of interest.
Signal-To-Noise
For each imaging mode, plots are provided to estimate the signal-to-noise (S/N) for a representative source. The first figure shows S/N for point sources (for two different gains for the CCD). The second figure shows S/N for uniform extended sources of area 1 arcsec2 and 0.2 arcsec2.
The different line styles in the S/N figures delineate regions where different sources of noise dominate. A particular source of noise (read noise for example) is presumed to dominate if it contributes more than half the total noise in the observations.
To the left of the vertical line in the S/N plots, the count rate from the source exceeds the 100 counts sec-1 pix-1 local count rate limit. This is computed from the on-orbit measured PSF, which gives 6 to 14% of the flux in the central pixel. The bright-object screening limits in Table 14.38 use the more conservative (for this purpose) estimate of 25% of the flux in the central pixel.
The point-source S/N figures are shown for average sky levels (i.e.,the `average zodiacal+average earthshine' background level used in the STIS ETC), and for sky levels during orbital night (i.e. average zodiacal + low earth). For the CCD the read noise has been computed assuming a number of readouts NREAD = integer (t / 1000 s), where t is the exposure time, with a minimum NREAD=2. That is, each exposure has a minimum CR-SPLIT=2. Different line styles in the figures are used to indicate which source of noise dominates.
For the CCD, the dominant sources of sky background are zodiacal light and scattered earthshine. The LOW-SKY requirement can be used to ensure that these backgrounds are kept as low or lower than the rates assumed for these plots. If your source falls within the sky-dominated portion of the figures, you may want to consider imposing the LOW-SKY requirement.
For the NUV-MAMA the sky background has about equal contributions from zodiacal light and OII 2470 Å emission on the day side of the orbit. On the night side, the OII 2470 Å emission is greatly reduced and the sky background is dominated by zodiacal light. In both cases the sky background is less than the dark current.
For the FUV-MAMA, the dominant source of background is geocoronal emission (see Table 6.6 and Table 6.7). The lines vary strongly from the day to night side of the orbit. For broad-band the contribution from the geocoronal lines can be minimized by using the F25QTZ filter, or observing with the DARKTIME special requirement.
In situations requiring more detailed calculations (non-stellar spectra, extended sources, other sky background levels, unknown target V magnitude, etc.), the STIS Exposure-Time Calculator should be used.
Follow these steps to use the signal-to-noise plots:
- Determine the AB magnitude of your source at the wavelength of interest. There are several ways to do this.
- Examine Table 14.1 and find AB
 for the desired spectral type and filter. Sum the V magnitude of the target and AB
for the desired spectral type and filter. Sum the V magnitude of the target and AB .
.
- Alternatively, compute ABMAG (=V+AB
 ) from the source flux, using the relation:
) from the source flux, using the relation:
 or
or

- Find the appropriate plot for the filter in question, and locate V+AB
 on the horizontal axis. Then read off the signal-to-noise ratio for the desired exposure time, or vice-versa.
on the horizontal axis. Then read off the signal-to-noise ratio for the desired exposure time, or vice-versa.
The "x" characters at the top of each plot indicate the onset of saturation, in the case of the CCD. The "x" shows where the total number of counts exceeds the 16-bit buffer size of 65,535.
We now give a sample S/N calculation using these plots. Consider a V=27 star of spectral class G2V, for which we want to obtain S/N = 20 with F28X50LP observing with the CCD. From Table 14.1 we find a correction AB = -0.21 to go from V magnitude to AB magnitude near the center of the F28X50LP bandpass. We thus have V+AB
= -0.21 to go from V magnitude to AB magnitude near the center of the F28X50LP bandpass. We thus have V+AB =26.79. We look at Figure 14.8 and find this value on the horizontal axis and read up to find the curve that intersects the desired S/N. We find ~10,000 seconds are needed to reach S/N = 20 in conditions of low sky background.
=26.79. We look at Figure 14.8 and find this value on the horizontal axis and read up to find the curve that intersects the desired S/N. We find ~10,000 seconds are needed to reach S/N = 20 in conditions of low sky background.
Point Spread Functions
The final figures and table for each imaging mode contain information on the point-spread function. The encircled energy plots and tables are normalized to 1 at a radius of 1 arcsecond. In actuality about 10% of the light from a point source falls beyond this radius; however high S/N observations extending out to large radius exist for only a few modes from on-orbit data. The intensity vs. radius plots are normalized to a total integrated flux of 1. The PSF image is shown on a logarithmic intensity scale to enhance faint features in the wings of the PSF. Note the stellar like `ghost' at approximately 45 pixels left of the peak pixel in the NUVMAMA+Filter images. The ghost is a few tenths of a percent of the psf peak intensity. See Bowers (1997 HST Calibration Workshop) for a discussion of HST "breathing" effects on the PSF.
Table 14.1: Color Corrections AB to go from Johnson V Magnitude to AB Magnitude
to go from Johnson V Magnitude to AB Magnitude
| Spectrum |
F28x50
LP |
50CCD |
OIII |
OII |
NUV
MAMA |
NUV
ND3 |
NUV
ND5 |
NUV
QTZ |
NUV
CN270 |
NUV
MgII |
NUV
CN182 |
NUV
CIII |
FUV
MAMA |
FUV
ND3 |
FUV
ND5 |
FUV
QTZ |
FUV
SRF2 |
FUV
LYA |
| Sky |
-0.31 |
0.13 |
0.23 |
1.79 |
0.15 |
0.18 |
0.61 |
3.17 |
4.96 |
4.88 |
1.87 |
4.33 |
-2.53 |
-2.46 |
-2.46 |
11.83 |
-0.30 |
-3.72 |
| Sky (shadow) |
-0.18 |
0.17 |
0.17 |
1.36 |
0.74 |
0.78 |
1.10 |
4.13 |
3.61 |
3.55 |
2.55 |
6.01 |
-2.04 |
-1.97 |
-1.97 |
10.74 |
2.87 |
-3.32 |
| O5V |
0.48 |
-0.23 |
-0.13 |
-0.64 |
-1.59 |
-1.53 |
-1.37 |
-1.50 |
-1.21 |
-1.14 |
-1.69 |
-1.66 |
-2.07 |
-2.07 |
-2.06 |
-1.9 |
-1.99 |
-2.18 |
| B0V |
0.47 |
-0.15 |
-0.16 |
-0.59 |
-1.26 |
-1.21 |
-1.09 |
-1.19 |
-0.96 |
-0.90 |
-1.36 |
-1.30 |
-1.61 |
-1.62 |
-1.62 |
-1.62 |
-1.68 |
-1.46 |
| A0V |
0.27 |
0.26 |
-0.06 |
0.83 |
1.79 |
1.74 |
1.58 |
1.70 |
1.56 |
1.54 |
1.80 |
1.75 |
2.81 |
2.79 |
2.75 |
1.94 |
2.32 |
4.62 |
| A5V |
0.18 |
0.27 |
-0.02 |
0.97 |
2.67 |
2.54 |
2.17 |
2.51 |
2.20 |
2.12 |
2.82 |
2.61 |
5.90 |
5.95 |
5.76 |
4.21 |
5.31 |
9.00 |
| F2V |
-0.02 |
0.22 |
0.07 |
1.06 |
3.35 |
3.07 |
2.49 |
3.18 |
2.61 |
2.57 |
4.11 |
4.06 |
8.65 |
8.78 |
8.55 |
6.83 |
8.05 |
12.24 |
| G2V |
-0.21 |
0.16 |
0.17 |
1.34 |
4.45 |
4.00 |
3.09 |
4.28 |
3.77 |
3.54 |
6.49 |
6.65 |
14.77 |
14.88 |
14.54 |
12.93 |
14.16 |
18.56 |
| K0V |
-0.31 |
0.14 |
0.21 |
1.85 |
5.60 |
5.16 |
4.17 |
5.43 |
5.13 |
4.9 |
7.62 |
7.22 |
10.17 |
10.17 |
10.14 |
9.67 |
9.97 |
10.54 |
| M0V |
-0.97 |
-0.30 |
0.68 |
3.29 |
6.93 |
6.48 |
5.44 |
6.75 |
6.64 |
6.41 |
9.12 |
8.56 |
11.67 |
11.67 |
11.65 |
11.17 |
11.48 |
12.04 |
| M6V |
-1.78 |
-1.03 |
0.74 |
3.44 |
7.32 |
6.86 |
5.79 |
7.14 |
7.12 |
6.89 |
9.59 |
8.86 |
12.15 |
12.15 |
12.12 |
11.65 |
11.96 |
12.52 |
| O7I |
0.45 |
-0.04 |
-0.12 |
-0.57 |
-0.50 |
-0.50 |
-0.54 |
-0.49 |
-0.56 |
-0.59 |
-0.53 |
-0.50 |
-0.52 |
-0.53 |
-0.53 |
-0.68 |
-0.62 |
-0.34 |
| B0I |
0.38 |
-0.06 |
-0.10 |
-0.42 |
-0.71 |
-0.71 |
-0.67 |
-0.70 |
-0.68 |
-0.64 |
-0.72 |
-0.71 |
-0.75 |
-0.76 |
-0.76 |
-0.77 |
-0.85 |
-0.50 |
| F0III |
0.05 |
0.25 |
0.02 |
1.08 |
3.55 |
3.29 |
2.69 |
3.38 |
2.89 |
2.79 |
4.20 |
4.04 |
8.57 |
8.71 |
8.48 |
6.74 |
7.97 |
12.21 |
| G0III |
-0.26 |
0.15 |
0.18 |
1.58 |
5.34 |
4.89 |
3.92 |
5.16 |
4.82 |
4.67 |
7.34 |
6.92 |
9.90 |
9.89 |
9.87 |
9.39 |
9.70 |
10.27 |
| K2III |
-0.52 |
0.03 |
0.36 |
2.77 |
7.39 |
6.93 |
5.74 |
7.21 |
7.84 |
7.12 |
10.34 |
8.5 |
13.42 |
13.42 |
13.39 |
12.92 |
13.22 |
13.79 |
| M0III |
-0.98 |
-0.32 |
0.61 |
3.89 |
7.58 |
7.20 |
6.21 |
7.41 |
7.33 |
7.00 |
9.23 |
8.89 |
11.16 |
11.16 |
11.14 |
10.66 |
10.97 |
11.53 |
| M6III |
-2.66 |
-1.87 |
1.54 |
3.16 |
7.12 |
6.77 |
5.87 |
6.96 |
6.63 |
6.30 |
8.54 |
8.14 |
10.47 |
10.46 |
10.44 |
9.97 |
10.27 |
10.84 |
| Elliptical |
-0.61 |
-0.05 |
0.36 |
2.17 |
5.16 |
4.98 |
4.39 |
5.05 |
4.94 |
4.91 |
5.57 |
5.43 |
6.33 |
6.32 |
6.30 |
5.99 |
6.16 |
6.96 |
| Sa |
-0.56 |
-0.03 |
0.28 |
1.79 |
4.2 |
3.99 |
3.45 |
4.08 |
3.73 |
3.70 |
4.71 |
4.67 |
5.78 |
5.76 |
5.74 |
5.30 |
5.55 |
6.50 |
| Sb |
-0.55 |
-0.03 |
0.29 |
1.77 |
3.65 |
3.49 |
3.02 |
3.55 |
3.33 |
3.30 |
3.99 |
3.97 |
4.73 |
4.72 |
4.71 |
4.30 |
4.52 |
5.43 |
| Sc |
0.15 |
0.16 |
-1.62 |
-0.54 |
1.82 |
1.62 |
1.13 |
1.71 |
1.31 |
1.27 |
2.26 |
2.35 |
2.98 |
2.96 |
2.94 |
2.48 |
2.70 |
3.84 |
| Starburst E(B -V) =0.51 -0.60 |
-0.47 |
-0.06 |
-0.41 |
0.68 |
1.92 |
1.86 |
1.69 |
1.84 |
1.70 |
1.73 |
2.02 |
1.99 |
2.79 |
2.77 |
2.76 |
2.37 |
2.52 |
3.64 |
| Starburst E(B -V) <0.1 |
-0.11 |
0.07 |
-1.85 |
0.07 |
1.04 |
1.03 |
0.99 |
1.01 |
0.98 |
0.94 |
1.05 |
1.06 |
1.42 |
1.40 |
1.39 |
1.11 |
1.18 |
2.17 |
| Sun |
-0.19 |
0.19 |
0.21 |
1.40 |
4.67 |
4.23 |
3.35 |
4.49 |
3.95 |
3.87 |
6.53 |
6.57 |
12.31 |
12.38 |
12.31 |
11.68 |
12.67 |
11.62 |
| Vega |
0.29 |
0.25 |
-0.06 |
0.87 |
1.75 |
1.70 |
1.53 |
1.65 |
1.49 |
1.47 |
1.80 |
1.74 |
2.91 |
2.88 |
2.85 |
2.07 |
2.43 |
4.64 |


or f
:
For filters with redleaks, the pivot wavelength and FWHM correspond to the "in-band" region, and do not include the redleak.
).
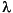
(see Chapter 6). For filters with redleaks this integration includes only the primary bandpass.






 to go from Johnson V Magnitude to AB Magnitude
to go from Johnson V Magnitude to AB Magnitude