6.7.3 Emission Line Sources

The signal-to-noise ratio calculation for point-like or extended emission-line sources is similar to that for continuum sources. However, the details of the calculation are different, because of the units used for the line flux, and because the flux is in a narrow line. The integrated filter efficiency is not relevant for the signal calculation; what matters is the total system throughput QT at the wavelength of the line, which can be determined from inspection of the figures in Appendix A. For lines near the center of the filter bandpasses the QTmax values from Table 6.1 can be used. The total signal expected for a point source of line strength F, expressed in erg s^-1 cm^-2, is S=2.28x10¹² t QT F, where t is the exposure time in seconds, and the wavelength of the line in Angstroms. Thus, H emission at 6563Å, with flux F=10^-16 erg s^-1 cm^-2, observed for 1000 seconds through the F656N filter (total system throughput QT=0.11 from the plots of F622W, F631N, F656N), will produce a total signal of S=165 electrons. The equivalent background per pixel is read-noise dominated: B=1+5.3²+4=33, for a background noise of ~6 electrons. The total noise is dominated by photon noise from the signal itself, and the signal-to-noise ratio achieved in this observation is ~27.

If the source is extended, the expected signal per arcsecond must be multiplied by the effective pixel area: 0.0099 arcsec2 for the WF, 0.0021 for the PC. For a line flux of, say, F = 10^-15 erg s^-1 cm^-2 arcsec^-2, this corresponds to 16 electrons in 1000 seconds for a WFC pixel. The noise is now dominated by the background, and the single-pixel signal-to-noise ratio is 16/(33 + 16)^1/2 ~ 2.3.

Extended Line Emission Source, Manual Calculation

We now consider a detailed example of a planetary nebula observed on the PC with the F502N filter. The nebula has a diameter of 5" and a total flux F=4x10^-13 erg s^-1 cm^-2 in the [OIII] 5007Å line. We want to estimate the SNR for an 1800s exposure, which will be CR-SPLIT.

First we must estimate the flux per square arcsecond. Using the nebula diameter, the average brightness is I = 2.0x10^-14 erg s^-1 cm^-2 arcsec^-2. From the plots in Appendix A, we see that QT=0.058. Using Equation 6.10 for the target count rate per pixel:

Next we estimate the SNR for each 900s sub-exposure using Equation 6.14 and Table 6.9. For this narrow filter the sky background can be ignored. We presume there is no background light from astrophysical sources:

Hence SNR=3.1 per pixel for each 900s sub-exposure. The SNR per pixel for the total 1800s is

The SNR for the entire nebula is this SNR per pixel times the square root of the number of pixels in the image, or ~460. In actuality, uncertainties in the photometric calibration and flat fields, would limit the SNR to ~100.

Extended Line Emission Source, On-Line Calculator

The above example could be calculated with the "Extended Source" form of the ETC program. The fill-out form would be completed as shown in Figure 6.7.

Figure 6.7: Extended Source Form for WFPC2 On-Line Exposure Time Calculator. Here the target is a galactic [OIII] 5007 line emission source and is observed on PC with filter F502N. SNR is computed for 1800s exposure.

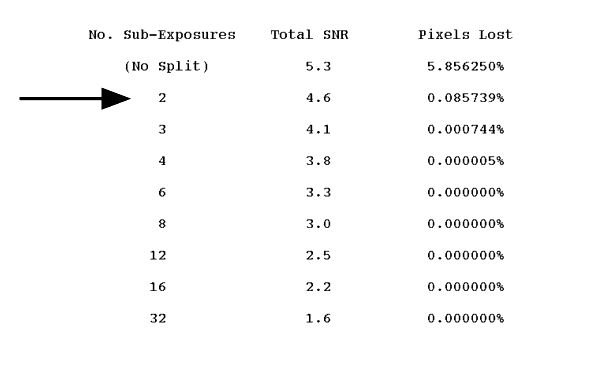
We have selected "[OIII] 5007" on the emission line menu, and have left the redshift (z) set to zero. The PC and F502N filter are selected. Note we have entered the exposure time as 1800s. Scrolling down through the output page we find a table of SNR for various CR-SPLITings of the exposure (See Figure 6.8:). "No. Sub-Exposures = 2" gives the answer we want, SNR=4.6 per pixel.

Figure 6.8: Sample Results on CR-SPLITing from WFPC2 On-Line Exposure Time Calculator Results Page.

Line Emission Point Source w/ LRF, Manual Calculation

In this example we consider an unresolved source of H emission in a galaxy at redshift z=0.22 with flux F=1.5x10^-16 erg s^-1 cm^-2. We want the SNR for a 2400s exposure without CR-SPLITing.

Since the redshift is significant, we cannot observe with the F656N filter. Instead we will use the Linear Ramp Filter (LRF). The observed wavelength will be 8007Å. From Table 3.7 we see that this will be observed using the FR868N filter on CCD WF3. Combining the LRF transmission from Figure 3.3 and the "WFPC2 + OTA System Throughput" from Figure 2.4 we estimate QT=0.054. We compute the count rate using Equation 6.4.

To estimate the SNR we use Equation 6.6, which assumes that PSF fitting will be used to analyze the image. Since the filter is narrow, we will ignore the sky emission. We use Table 6.6 for the WFC sharpness and also the read noise.

which is for an un-split 2400s exposure. The Poisson noise and background noises contribute nearly equally. For three such exposures over three orbits

Line Emission Point Source w/ LRF, On-Line Calculator

The above calculation can be performed using the ETC program. The "Point Source" form is used. "Emission Line" source and the "H 6563" line are selected; the redshift is set to 0.22. The program will automatically choose between PC and WFC, depending on the LRF setting. The least optimistic case of placing the object on a "pixel corner" is selected. The filter "LRF" is selected from the filter menu, and 8007Å is given for the central wavelength. The exposure time is specified as 2400s. (See Figure 6.9 for example of completed form.)

Figure 6.9: Point Source Form for WFPC2 On-Line Exposure Time Calculator. The target is an unresolved galaxy (z=0.22) nucleus with H line emission which is observed with LRF. SNR is computed for 2400s exposure.

The result is SNR=13.1 for the un-split 2400s exposure ( Figure 6.10), which is comparable to the manual calculation of SNR=14.

Figure 6.10: Sample Output for WFPC2 On-Line Exposure Time Calculator.