6.7.1 Point Sources

Simple Star, Manual Calculation, PSF Fitting

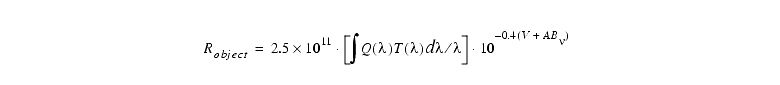
We begin with the simple example of a V=20 star of spectral class G0. We want to observe with the PC using filter F555W. The star is somewhere near the ecliptic pole. We want to know the SNR for a 1200s CR-SPLIT exposure. Default ATD-GAIN=7 is used. We plan to use PSF fitting to analyze the data.

First we estimate the count rate for our target. Consulting Equation 6.2, Table 6.1, and Table 6.2 we have:

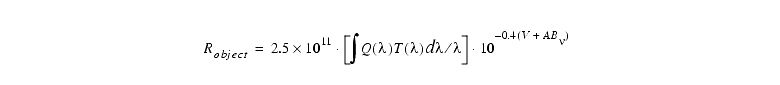
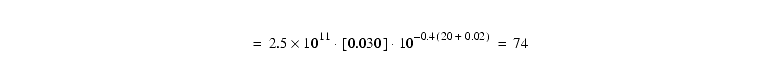
in units of e^- s^-1. Next we fill out Equation 6.6. To keep things simple we just use values from Table 6.6, and get the sky count rate from Table 6.4. There is no background light (i.e. no superposed galaxy), so Pbackground=0. The exposure time t=600 for each exposure of the CR-SPLIT:

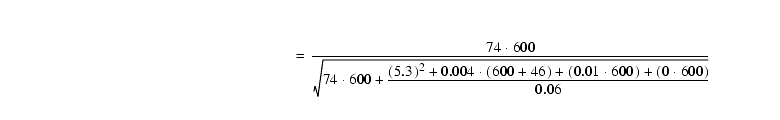
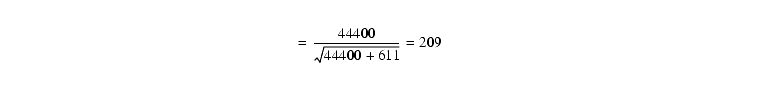
The SNR for the total 1200s exposure, i.e. both halves of the CR-SPLIT, would simply be:

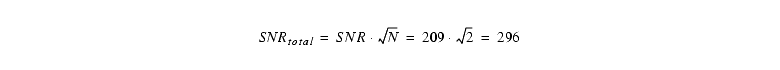
At these high SNR levels, it is likely that flat fielding would limit the photometric accuracy, rather than the noise. If we have a look at the terms in the SNR equation, we can see that the Poisson noise dominates; the term containing the sharpness and background noise sources is unimportant.

Just for fun, let us see what happens if we keep everything the same, but give the target V=25. Now we have Robject=0.74 e^- s^-1, and:

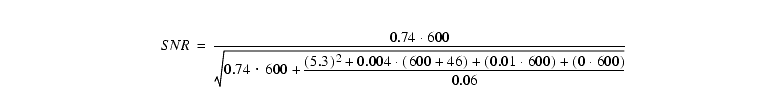
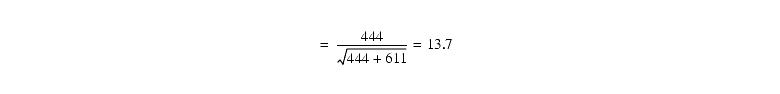
We see that now the term with the background noise (in particular, the read noise) limits the SNR. For the full 1200s exposure the SNRtotal=19.3.

Simple Star, Manual Calculation, Aperture Photometry

What if we now want to observe this same V=25 star, but we plan to reduce the data by measuring counts in a 0.5" radius aperture? We now use Equation 6.7 instead, consult Table 6.7 for the encircled energy f(r), and note that 0.5" corresponds to r=11.6 PC pixels:

Apparently using aperture photometry with a 0.5" radius aperture reduces the SNR by a factor ~4 as compared to PSF fitting, for this background limited case.

Simple Star, SNR Plots, PSF Fitting

We now repeat the first calculation above for the V=20 star using the SNR plots in Appendix B. We look up the G0 spectral class and F555W filter (5500Å) in Table B.1, and obtain AB=0.02. For the V=20 star, we thus have V+AB=20.02. We look at Figure B.10 and find this value on the horizontal axis. We locate exposure time 600s (one-half of the total 1200s CR-SPLIT exposure), and find SNR~200. For the total 1200s exposure the SNR would be .

Simple Star, On-Line Calculator, PSF Fitting

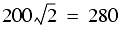The above calculation for a V=20 G0 star may also be performed using the WFPC2 Exposure Time Calculator program, which is available on the WFPC2 WWW pages at:

http://www.stsci.edu/instruments/wfpc2/Wfpc2_etc/wfpc2-etc.html
 

Figure 6.2: Sample Fill-out Form for WFPC2 On-Line Exposure Time Calculator..

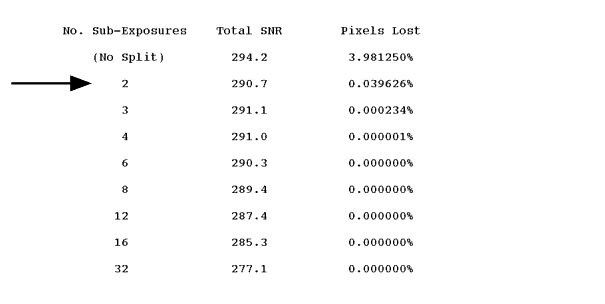
To use this program, access the above address with Netscape, or a similar program. Once in the WFPC2 area, select the "Software Tools" page, and then the "ETC" page. For the first example above, choose the "Point Source" form and complete it as shown in Figure 6.2 for the 600s sub-exposure. Then click the "calculate" button and after a few seconds the result is displayed ( Figure 6.3). The answer, SNR=208, is comparable to that obtained by the manual calculation above for the 600s sub-exposure (SNR=209). Alternatively, one can input the total exposure time (1200s), and then use the result farther down the output page for "No. Sub-Exposures = 2" (see Figure 6.4), thereby obtaining SNR=291 for the total 1200s CR-SPLIT exposure.

Figure 6.3: Sample Results from WFPC2 On-Line Exposure Time Calculator.

Figure 6.4: Sample Results on CR-SPLITing from WFPC2 On-Line Exposure Time Calculator Results Page.

Star Superposed on Galaxy, Manual Calculation

We now consider a B=25 point source of spectral class B0, which is superposed on an elliptical galaxy with V=22 mag arcsecond^-2. We want to compute the SNR obtained from a one-orbit (40 min.) non-CR-SPLIT observation in filter F300W on the WFC. PSF fitting will be used for the photometry.

We begin by computing the total count rate for the target. Using Table Table 6.2 we see that this target will have V=25.31. From Table 6.1 we obtain the filter efficiency and mean wavelength. Interpolating by mean wavelength in Table 6.2 we obtain AB=-0.83 for the B0 star. Using Equation 6.2 we have:

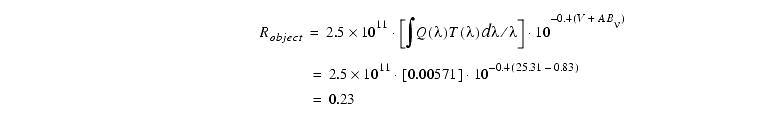
in units of e^- s^-1. Next we consider the background light from the superposed galaxy. We set V=22 mag arcsecond^-2 in Equation 6.11, and AB=3.63 for a gE galaxy at =3000Å (filter F300W) from Table 6.2. Hence the count rate per pixel due to the background light is:

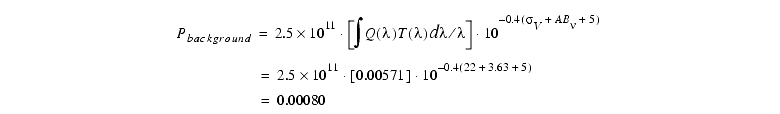
For the sky background, we note that Table 6.4 has no entry for F300W, so that the sky must be unimportant. If we wanted to calculate it anyway, as a check, we would use Table 6.3 for the sky brightness, Table 6.2 for the sky's AB, and again Equation 6.11. We will assume the target is near the ecliptic pole.

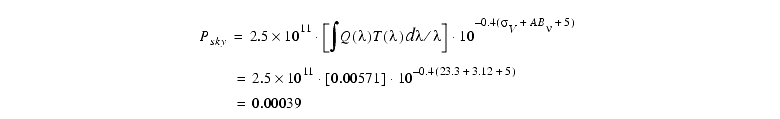
For the sharpness function we will use "pixel corner" values (least optimistic choice) from Table 6.5. Using read noise and dark current from Table 6.6, and Equation 6.6 for point source SNR:

for this single exposure. The SNR for multiple 40 min. exposures would be simply 17.9(N1/2), where N is the number of exposures.

Star Superposed on Galaxy, On-Line Calculator

The above calculation could also be performed with the on-line WFPC2 Exposure Time Calculator. One would select the "Point source + stellar background" form, and complete it as in Figure 6.5, and then click on "calculate." Figure 6.6 shows some of the results.

Figure 6.5: Point Source + Stellar Background Fill-out Form for WFPC2 On-Line Exposure Time Calculator. SNR is calculated for B=25 star (class B0) superposed on an elliptical galaxy (gE) with V=22. WFC is used with F300W.

Figure 6.6: Sample Output from WFPC2 On-Line Exposure Time Calculator.