5.11 Optical Distortion

The geometric distortion of WFPC2 is complex since each individual CCD chip is integrated with its own optical chain (including corrective optics), and therefore each chip will have its own different geometric distortion. Apart from this, there is also a global distortion arising from the HST Optical Telescope Assembly (Casertano and Wiggs 2001).

Early attempts to solve the WFPC2 geometric distortion were made by Gilmozzi et al. (1995), Holtzman et al. (1995), and Casertano et al. (2001), using third order polynomials for all chips in the PC system, i.e. the coordinates X,Y were transformed into one meta-chip coordinate system and fitted to find the offsets, rotation and scale for each of the four chips. These early meta-chip solutions failed to constrain the skew-related linear terms, which actually are responsible for ~0.25 pix residual distortion. These solutions did not have on-orbit data sets which were rotated with respect to each other.

In 2003, Anderson and King derived a substantially improved geometric distortion solution for WFPC2 in the F555W filter. First, the measured positions Xobs,Yobs were normalized over the range of (50:800) pixels excluding the pyramid edges (Baggett, S., et al. 2002) and adopting the center of the solution at (425,425) with a scale factor of 375, i.e:

The final solution was presented as a third-order polynomial:

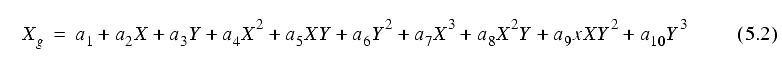
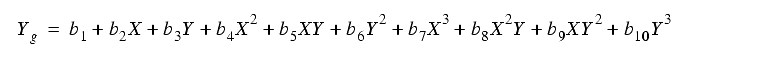
where Xg and Yg are the corrected coordinates.

The coefficients of the polynomials for F555W filter are given in Table 5.6 (Anderson and King 2003).

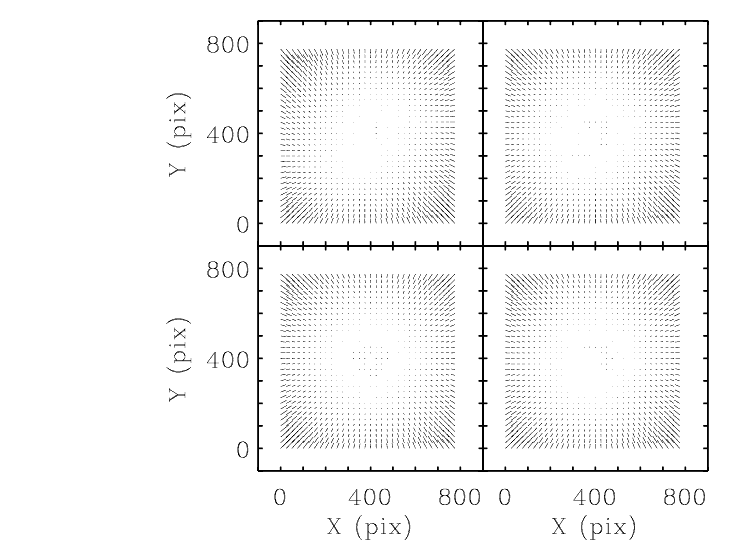
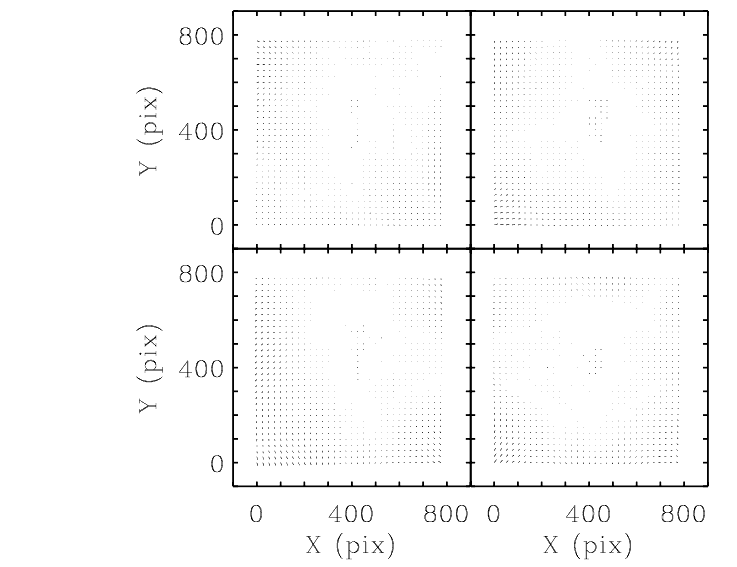
Figure 5.16 shows the vector diagram of the geometric distortion in filter F555W.

Table 5.6: Polynomial Coefficients of the Geometric Distortion for F555W.

	APC	AWF2	AWF3	AWF4	BPC	BWF2	BWF3	BWF4
1	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
2	0.000	0.000	0.000	0.000	0.418	0.051	-0.028	0.070
3	0.000	0.000	0.000	0.000	-0.016	-0.015	-0.036	0.059
4	-0.525	-0.624	-0.349	-0.489	-0.280	-0.038	-0.027	-0.050
5	-0.268	-0.411	-0.353	-0.391	-0.292	-0.568	-0.423	-0.485
6	-0.249	-0.092	0.009	-0.066	-0.470	-0.444	-0.373	-0.406
7	-1.902	-1.762	-1.791	-1.821	-0.011	0.003	0.004	-0.015
8	0.024	0.016	0.006	0.022	-1.907	-1.832	-1.848	-1.890
9	-1.890	-1.825	-1.841	-1.875	0.022	0.011	0.006	0.022
10	-0.004	0.010	0.021	-0.006	-1.923	-1.730	-1.788	-1.821

Figure 5.16: The geometric distortion map for F555W filter using the Anderson and King solution (2003). The size of the longest arrows are 6.29 pixel for the PC (in PC pixels) and ~6 pixel for WF cameras (in WF pixels). The panels correspond to PC - upper right; WF2 - upper left; WF3 - lower left and WF4 - lower right. The size of the residuals are scaled by a factor of 10 relative to the pixel coordinates.

Trauger et al. (1995) showed that the geometric distortion for WFPC2 also depends on wavelength. This is due to the refractive MgF2 field-flattener lens in front of each CCD. They computed the wavelength-dependent geometric distortion by analyzing the results of ray tracing, where the coefficients were represented as a quadratic interpolation function of the refractive index of the field-flattener lenses. Kozhurina-Platais et al. (2003), using the Anderson and King methodology (2003), derived the geometric distortion solutions for two other filters: F814W and F300W. Figure 5.17 presents the difference in distortion between F555W and F300W, which clearly indicates a large amount of distortion in F300W, especially at the corners of the chips. An average increase of distortion in the F300W filters is ~3%, or 0.18 pixels in PC and 0.25 pixels in WF cameras. In contrast, there is only a small ~1% difference in distortion between F555W and F814W. Figure 5.18 presents the difference between the filters F555W and F814W. The coefficients of the polynomials for filters F300W and F814W are given in Table 5.7 and Table 5.7, respectively.

Figure 5.17: Difference in the distortion correction between F555W and F300W (F555W-F300W). The size of the longest arrows are 0.18 pixel for PC (in PC pixel) and 0.25 pixel for WF cameras (in WF pixels). The panels are the same as in Figure 5.16, except the size of the residuals are scaled by a factor of 300.

Figure 5.18: Difference in the distortion correction between F555W and F814W. The small amount of these differences along with fairly random pattern changing from chip to chip indicate that the differences are very small, if present at all. The size of the longest arrow is 0.04 PC pixels for the PC, and ~0.05 pixels for the WF cameras. The panels are the same as in Figure 5.16, except the size of the residuals are scaled by a factor of 300.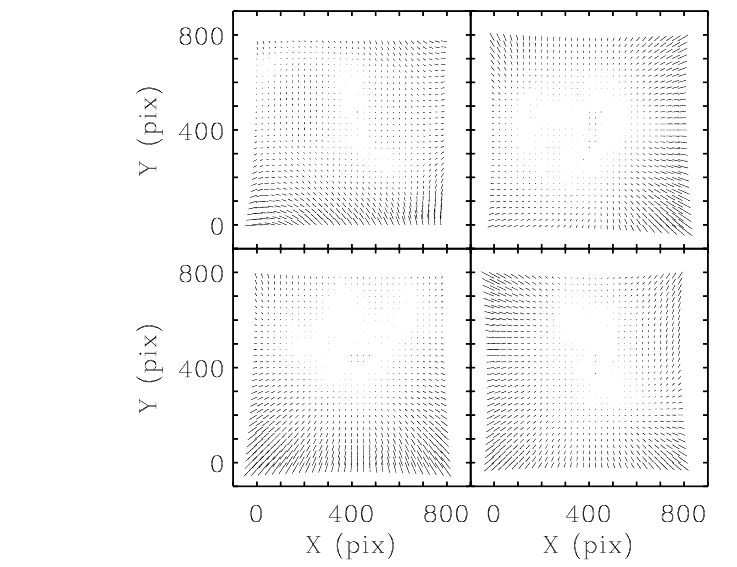

Application of the distortion coefficients are straight forward. To correct for geometric distortion, the measured raw coordinates should be normalized as in the equation 5.1 on page 144. Then equation 5.2 on page 144 should be used, employing the coefficients from Table 5.6, Table 5.7 or Table 5.8, depending on the filter used. Finally, the corrected coordinates Xg, Yg should then be shifted back to the natural system of the detector, with proper orientation and scale, specifically:

The constant terms a1 and b1 are offsets (or zero-points) between any two frames and can be ignored for most purposes. The linear coefficients a2 and b3 represent the plate scale and can be found in Anderson and King (2003) and Kozhurina-Platais et al. (2003). The FORTRAN code developed by Anderson which correct the measured coordinates X and Y can be down-loaded from

http://www.stsci.edu/instruments/wfpc2/Wfpc2_memos/anderson
king_distortion_routine.txt
 

The same program could be used to correct for distortion in filters F300W and F814W, using the coefficients from Table 5.7 or Table 5.8, respectively.

Table 5.7: Polynomial Coefficients of the Geometric Distortion for F300W.

	APC	AWF2	AWF3	AWF4	BPC	BWF2	BWF3	BWF4
1	0.374±0.047	0.149±0.010	-0.142±0.014	-0.072±0.012	0.267±0.021	-0.164±0.014	-0.113±0.011	0.174±0.014
2	0.999±0.091	0.999±0.009	0.999±0.009	0.999±0.015	0.480±0.069	0.042±0.010	-0.028±0.008	0.048±0.006
3	0.055±0.032	0.001±0.009	0.006±0.008	-0.027±0.009	0.999±0.101	0.999±0.010	0.999±0.013	0.999±0.012
4	-0.547±0.035	-0.687±0.009	-0.363±0.005	-0.469±0.007	-0.298±0.113	-0.043±0.006	-0.019±0.005	-0.078±0.005
5	-0.255±0.035	-0.394±0.008	-0.299±0.007	-0.386±0.010	-0.265±0.051	-0.592±0.011	-0.419±0.005	-0.489±0.006
6	-0.235±0.078	-0.098±0.007	0.015±0.008	-0.079±0.005	-0.479±0.052	-0.453±0.018	-0.335±0.006	-0.386±0.008
7	-1.937±0.139	-1.837±0.019	-1.838±0.011	-1.874±0.022	-0.079±0.126	0.006±0.015	0.007±0.008	-0.028±0.008
8	0.003±0.067	0.034±0.016	0.003±0.013	0.054±0.012	-1.913±0.113	-1.877±0.024	-1.891±0.014	-1.950±0.014
9	-1.909±0.056	-1.869±0.010	-1.875±0.015	-1.936±0.009	-0.021±0.083	0.040±0.016	0.016±0.008	0.049±0.018
10	-0.039±0.064	0.001±0.007	0.021±0.012	-0.011±0.017	-1.863±0.148	-1.773±0.018	-1.846±0.016	-1.852±0.014

Geometric distortion not only affects astrometry but photometry as well, since it induces an apparent variation in surface brightness across the field of view. The effective pixel area can be derived from the geometric distortion coefficients, and is presented in Figure 5.19. The pixel area map correction is necessary since the flat fields are uniformly illuminated, and do not explicitly conserve the total integrated counts for a discrete target, whereas the geometric distortion conserves the total counts and redistributes the counts on the CCD chip. Thus, for precise stellar photometry the raw flat fielded images require a correction for the pixel area -- raw flat-fielded images should be multiplied by the pixel area map so as to restore the proper total counts of the target. The pixel area map is available as a fits file in the HST archive. (Some additional discussion of the pixel area correction can be found in the ACS Instrument Handbook for Cycle 14.)

Figure 5.19: A map of the effective pixel areas of the WFPC2 chips. The areas are normalized to unity at the center of each chip. The contours are shown at half present level. The panel corresponds to PC -upper right; WF2 - upper left; WF3 - lower left and WF4 - lower right.